Decoding Similarity Search with FAISS: A Practical Approach
I am preparing for a series of conference talks and workshops on Retrieval Augmented Generation. With my strong information retrieval (search) background, I have been working on vector-based technologies. I found some excellent resources on using FAISS from James Briggs.
In this blog post, you read about FAISS and your options for implementing similarity search using FAISS. I decided to use the Python Notebook approach to enable you to tag along.
Semantic Search
Before we dive into FAISS, let us spend some time on Semantic Search. What is Semantic Search? I assume you are used to search engines on websites and most likely Google. Most of the site search engines use search engines like Elasticsearch, OpenSearch, and Solr. Most websites may not even be. A lot of sites still use SQL queries to perform searches. Most of these engines use some form of Lexical search or keyword matching. As a user, you must type precisely the terms known in the data. More advanced engines use mechanisms to overcome typos and synonyms. These engines need help understanding what you are talking about. They need to get the semantic meaning of the words you use in the query.
We have all been trained by using these websites only to enter a few words in a search bar. If you, as a company, are lucky, your users will try other words when you do not present them with the right results. Suppose you better understand the semantic meaning of the user and match concepts rather than keywords. In that case, you can present much better results, positively impacting your user experience and business outcome.
We need a way to match concepts, but how do we determine this meaning or similarity between concepts in pieces of text? One answer is transforming text into mathematical representations, typically vectors. Once our data is represented as vectors in a multi-dimensional space, finding similar items becomes a matter of calculating distances between these vectors. Here’s where algorithms like k-nearest neighbors (kNN) come into play.
Similarity search using kNN
Calculation is more straightforward with numbers than with text. The moment we started talking about calculating distances, we stepped over many concepts. First, we need to transform text into a vector of numbers. Second, we need to calculate distances between these vectors of numbers. We discuss converting text into numbers in the section about embeddings.
For now, imagine we have the vectors. In the image below, we simplified them into a two-dimensional space. However, in reality, this is a lot higher. The vectors we work with have 1536 dimensions. More about that later in the embeddings section.
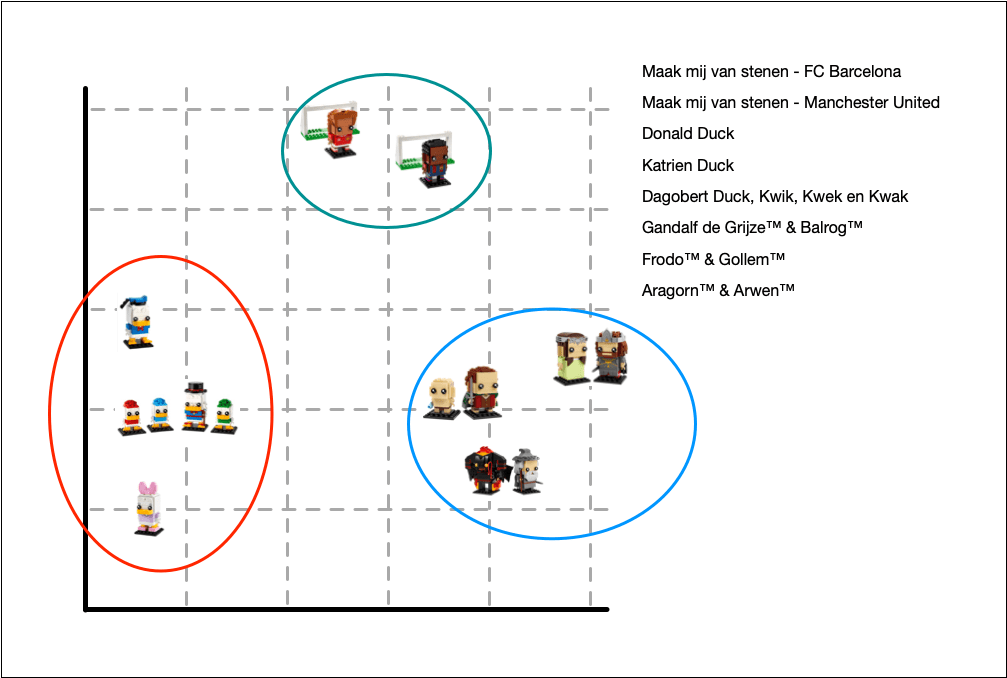
There are different formulas to calculate the similarity between vectors. Examples are l2, cosine similarity, and inner product.
To get an intuition on the distance metrics, below you get an idea for calculating the similarity between the vector for voetbal and Frodo & Gollem.
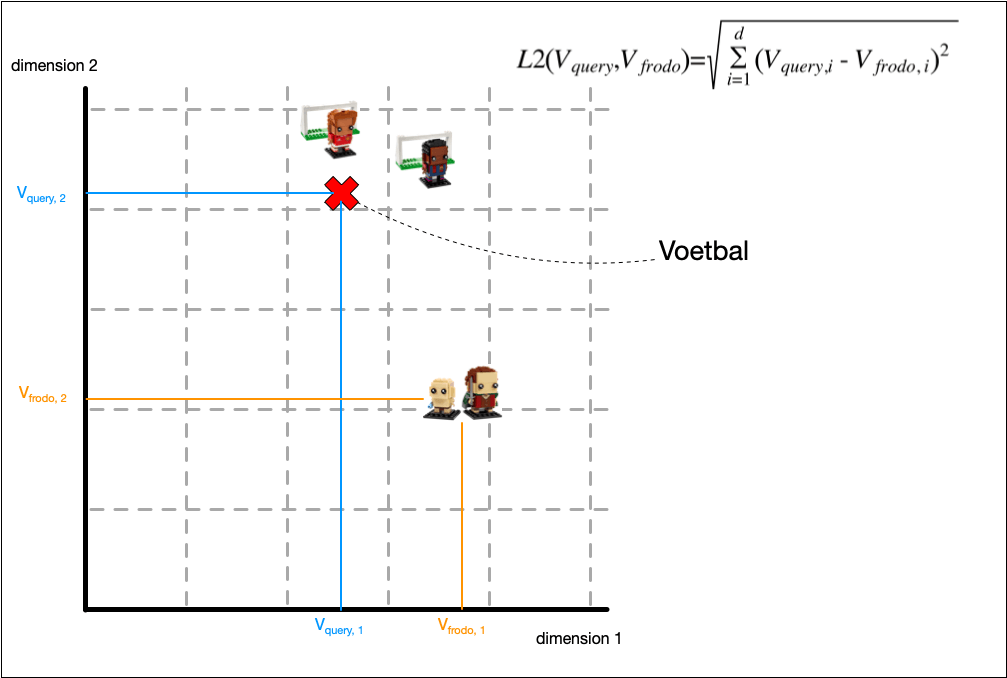
Now, we can compare two vectors and calculate how similar they are. We can use brute force and exact calculations to find the most similar vectors. This is okay if you have less than 100k documents. Approximate Nearest Neighbours is available for speed. It will be less accurate. You trade in accuracy for speed. For most models, you can tune this balance. We discuss ANN, HNSW, IVF in another section.
The next sections give more background information on the topics discussed here. Together with the Notebook, these sections give you a fair understanding of working with vector similarity.
Embeddings
Did you look at the Notebook? In one block, we create a method called create_embedding. The method uses the OpenAI API. Through this API, we use the model text-embedding-ada-002. This model accepts text and outputs a vector of dimension 1536.
Training such a model is easier than training Large Language Models. However, taking an existing embedding model is usually easier with a larger corpus of texts. Training your custom model can improve results if you have a corpus with many non-familiar words. Techniques like word2vec that train on guessing missing words or next words are well documented. I like this tutorial from Tensorflow.
Distance Metrics
The similarity between two vectors is calculated using a distance metric. You can choose different metrics. L2 is a good first choice. Similarity is used a lot as well. The inner product is another good choice. I am not going into all the details. Choosing the best model is a matter of testing them.
L2 or Euclidean distance is also called the straight line distance between two vectors. Values must be normalized. The metric performs poorly if the dimensions increase to tens of thousands.
Cosine similarity is a good second choice that only measures the angle between vectors. It does not consider the lengths of vectors.
The inner product, or dot product, is a specialization of the cosine similarity. Faiss uses this next to L2 as a standard metric. IP performs better on higher-dimension vectors.
The Weaviate documentation has a nice overview of distance metrics.
FAISS Indexes
The beginning of this blog post shows how to work with the Flat index of FAISS. This index is called exhaustive, and the results are exact. They are exact, as we determine the distance for all available vectors to the query’s vector. You can imagine that the performance for such a query becomes a problem with too many vectors. If speed is important, we need another index. Meet the approximate indexes. These indexes are not exact anymore, but they are faster. They have a way of limiting the scope of the search to perform. Now, the trick is to find the best balance between performance and quality of results.
HNSW - Hierarchical Navigable Small World
An approach that uses a graph to find the vector that best matches the query vector. The graph vertices have several friends. The graph traverses the friend closest to our query if it is closer to our query than the current vector. Combining multiple graphs that become more accurate per layer creates a hierarchy of graphs. The highest layer is the entry point. When we reach the closest distance, we go to the connected lower layer connected to the vertex in the top layer.
We can configure the amount of friends each vertex has. More friends mean higher accuracy, but lower performance. Imagine you are searching for a kitchen. You ask five companies for an offer and choose the lowest. If you ask 100 companies for their price, you can get a better price. It will take a lot of effort, though.
You can read more about HNSW and Faiss in this post from Pinecone.
IVF - Inverted File System or Index
IVF is an interesting clustering technique to select a subset of the vectors to calculate the best matches from. It uses a Voronoi diagram to select cells with vectors to consider. The idea is to have several centroids in cells with vectors closer to that centroid than any other centroid. Next, we find the most similar centroid to the query and select that cell to find the most similar vectors.
Sometimes, we miss a similar vector right at a cell’s border. This hurts the accuracy of the index. Therefore, we can select multiple cells to limit the chance of missing a good vector. That does increase the latency of the index. So again, we have to find the right balance.
Final words
Working with vector stores like Weaviate, Amazon OpenSearch Service, and Pinecone gives you much power. Without the knowledge of the technology supporting these data stores, you cannot create the best-performing solution. You must understand the trade-off between performance and accuracy - the difference between exhaustive similarity calculation and exact results with approximate similarity.
Therefore, when working with one of those vector stores, read the documentation for the right parameters to find the optimal balance of accuracy and performance for your specific application.
References
Pinecone has a nice series of posts bundled in Faiss: The Missing Manual.
James Briggs has created some incredible YouTube videos. His series about similarity search accompanies the posts from the link above.
Nice overview of vector search with Weaviate that explains most concepts in the Weaviate context.
Extensive documentation for the kNN plugin in OpenSearch.
Meer weten over wat wij doen?
We denken graag met je mee. Stuur ons een bericht.
